4.2.1 Tipos de matrices (cuadrada, rectangular, triangular, matriz identidad, matriz transpuesta). |
| El objetivo general de esta materia Matemáticas II es brindarnos nuevos conocimientos de nuevos temas aplicados en ella, como: Tipos de matrices (cuadrada, rectangular, triangular, matriz identidad, matriz transpuesta). |
Existen diversos tipos y clasificaciones de matrices:
Contenido
- 1 Matríz cuadrada
- 2 Matriz Rectangular
- 3 Matriz Vertical
- 4 Matriz Columna
- 5 Matriz Horizontal
- 6 Matriz Fila
- 7 Matriz Diagonal
- 8 Matriz Escalonada
- 9 Matriz Triangular superior
- 10 Matriz Triangular inferior
- 11 Matriz Identidad
- 12 Matriz Nula o Matriz Cero
- 13 Matriz Opuesta
- 14 Matriz Traspuesta
- 15 Matriz Simétrica
- 16 Matriz Antisimétrica
- 17 Matriz Ortogonal
- 18 Matriz Normal
- 19 Matriz Conjugada
- 20 Matriz Invertible
- 21 Matriz Singular o Degenerada
- 22 Matriz Permutación
- 23 Matrices iguales
- 24 Matriz Hermitiana
- 25 Matriz definida positiva
- 26 Matriz Unitaria
- 27 Submatriz
- 28 Resto del capítulo Matrices
Matríz cuadrada
Se dice que una matriz A es cuadrada si tiene el mismo número de filas que de columnas. Ejemplos de matriz cuadrada:Puede ser una matriz con valores

O también una matríz con subíndices (Genérica)

Puede ser de otro tamaño e incluso con variables
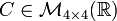
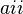 .
.Se llama diagonal secundaria a la diagonal del cuadrado que no es la principal, tiene por extremos los elementos
 y
y 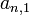 , como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo
, como características, todos los elementos tienen la particularidad que sus subíndices suman (n+1), por ejemplo 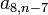 , donde 8 + (n - 7 ) = n + 1.
, donde 8 + (n - 7 ) = n + 1.Matriz Rectangular
Es aquella matriz que no es cuadrada, esto es que la cantidad de filas es diferente de la cantidad de columnas.Puede ser de dos formas; vertical u horizontal.
Matriz Vertical
Es aquella que tiene más filas que columnas.Matriz Columna
Caso especial de matriz vertical que posee una sola columna.Matriz Horizontal
Es aquella que tiene más columnas que filas.Matriz Fila
Caso especial de matriz horizontal que posee una sola fila.Matriz Diagonal
Se llama diagonal principal de una matriz A a la diagonal formada por los elementos aij.Matriz diagonal, matriz cuadrada donde sus elementos
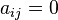 si
si  .
.La matriz identidad es una matriz diagonal.
Una matriz diagonal es una matriz cuadrada en que las entradas o valores son todos nulas salvo en la diagonal principal, y éstos incluso pueden ser nulos o no. Otra forma de decirlo es que es diagonal si todos sus elementos son nulos salvo algunos de la diagonal principal. Ejemplos de matrices Diagonales:
Puede ser una matriz con valores

O también una matríz con subíndices (Genérica)

Puede ser de otro tamaño e incluso con variables
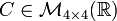
Matriz Escalonada
Es toda matriz en la que el número de ceros que precede al primer elemento no nulo, de cada fila o de cada columna, es mayor que el de la precedente.Puede ser escalonada por filas o escalonada por columnas.
Matriz Triangular superior
Se dice que una matriz (cuadrada) es triangular superior si todos los elementos que están por debajo de la diagonal principal son nulos.Matriz Triangular inferior
Se dice que una matriz es triangular inferior si todos los elementos que están por encima de la diagonal principal son ceros.Matriz Identidad
Se llama matriz identidad de orden n y se nota In a una matriz cuadrada de orden n en la que los elementos de la diagonal principal son 1 y el resto 0.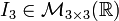
La matriz identidad puede ser de cualquier tamaño, siempre y cuando sea cuadrada
Matriz Nula o Matriz Cero
Una matriz cero o matriz nula es una matriz con todos sus elementos nulos, o sea de valor cero. Algunos ejemplos de matrices nulas son:Matriz Opuesta
Teniendo una matriz determinada, se llama matriz opuesta de la antes mencionada a aquella que tiene por elementos los opuestos de los elementos de la matriz original.Matriz Traspuesta
Matriz traspuesta (At). Se llama matriz traspuesta de una matriz A a aquella matriz cuyas filas coinciden con las columnas de A y las columnas coinciden con las filas de A.- Para una matriz
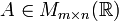 , se define la matriz transpuesta de
, se define la matriz transpuesta de  , denotada por
, denotada por 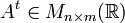 , como
, como 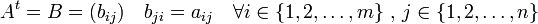 . Es decir, las filas de la matriz
. Es decir, las filas de la matriz  corresponden a las columnas de
corresponden a las columnas de  y viceversa.
y viceversa.
Matriz Simétrica
Una matriz es simétrica cuando es una matriz cuadrada, y es igual a su traspuesta.Matriz Antisimétrica
Una matriz es antisimétrica cuando es una matriz cuadrada, y es igual a su traspuesta de signo opuesto, siendo los elementos de la diagonal principal nulos; de valor cero.Matriz Ortogonal
Una matriz ortogonal es una matriz cuya matriz inversa coincide con su matriz traspuesta.Matriz Normal
Sea A matriz compleja cuadrada, entonces es una matriz normal si y sólo siMatriz Conjugada
Una Matriz conjugada es el resultado de la sustitución de los elementos de una matriz por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian su signo.
por sus valores conjugados. Es decir, la parte imaginaria de los elementos de la matriz cambian su signo.Ejemplo de matrices conjugadas
Matriz Invertible
También llamada matriz , no singular, no degenerada, regular.Una matriz cuadrada A de orden n se dice que es invertible si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A−1, tal que
- AA−1 = A−1A = In,
La inversión de matrices es el proceso de encontrar la matriz inversa de una matriz dada.
Matriz Singular o Degenerada
También llamada no regular. Una matriz es singular si y solo si su determinante es cero.Matriz Permutación
La matriz permutación es la matriz cuadrada con todos sus n×n elementos iguales a 0, excepto uno cualquiera por cada fila y columna, el cual debe ser igual a 1.Matrices iguales
Se dice que dos matrices A y B son iguales si tienen la misma dimensión y son iguales elemento a elemento, es decir, aij=bij i=1,...,n j=1,2,...,m.Matriz Hermitiana
Una matriz Hermitiana (o Hermítica) es una matriz cuadrada de elementos complejos que tiene la característica de ser igual a su propia traspuesta conjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j.Matriz definida positiva
Una matriz definida positiva es una matriz hermitiana que en muchos aspectos es similar a un número real positivo.Matriz Unitaria
Es una matriz compleja U, de n por n elementos, que satisface la condición: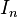 es la matriz identidad y
es la matriz identidad y  es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición implica que una matriz U es unitaria si tiene inversa igual a su traspuesta conjugada
es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición implica que una matriz U es unitaria si tiene inversa igual a su traspuesta conjugada  .
.Una matriz unitaria en la que todas las entradas son reales es una matriz ortogonal.
Submatriz
A partir de una Matriz M, se llama submatriz M' a toda matriz obtenida suprimiendo p filas y q columnas en M. Si M es de orden mxn, M' será de orden (m-p)x(n-q), es decir con p filas menos y q columnas menos. Es evidente que p < m ; q < n.Resto del capítulo Matrices
- Conceptos previos
- Concepto de Matriz
- Determinante de una matriz
- Tipos de matrices
- Suma de matrices
- Sistema de ecuaciones lineales
- Regla de Cramer
| (2015). Tipos de matrices (cuadrada, rectangular, triangular, matriz identidad, matriz transpuesta).En: wikiboo… Buscado elMartes, 10 de noviembre de 2015 Disponible en: https://es.wikibooks.org/wiki/Matem%C3%A1ticas/Matrices/Tipos_de_matrices |
| ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon. |


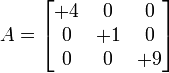
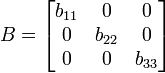

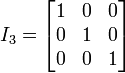
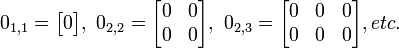
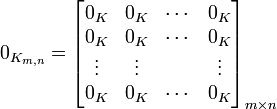
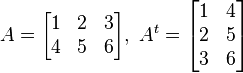

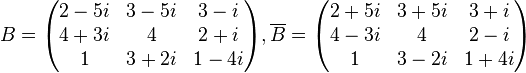

0 comentarios:
Publicar un comentario