3.2 Teorema Fundamental del cálculo. |
| El objetivo general de esta materia Matemáticas II es brindarnos nuevos conocimientos de nuevos temas aplicados en ella, como: Teorema Fundamental del cálculo. |
El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función acotada e integrable (siendo continua o discontinua en un número finito de puntos) verifica que la derivada de su integral es igual a ella misma. Este teorema es central en la rama de las matemáticas denominada análisis matemático o cálculo.
El teorema es fundamental porque hasta entonces el cálculo aproximado de áreas -integrales- en el que se venía trabajando desde Arquímedes, era una rama de las matemáticas que se seguía por separado al cálculo diferencial que se venía desarrollando por Isaac Newton, Isaac Barrow y Gottfried Leibniz en el siglo XVIII y dio lugar a conceptos como el de las derivadas. Las integrales eran investigadas como formas de estudiar áreas y volúmenes, hasta que en ese punto de la historia ambas ramas convergieron, al demostrarse que el estudio del "área bajo una función" estaba íntimamente vinculado al cálculo diferencial, resultando la integración, la operación inversa a la derivación.
Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la integral indefinida de la función al ser integrada.
Índice
Intuición geométrica
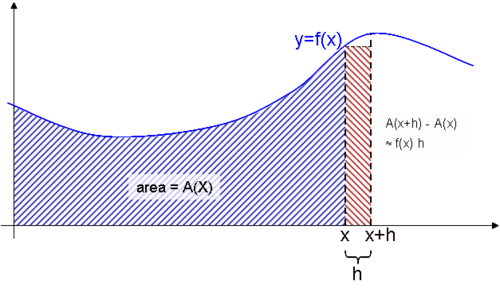
El área rayada en rojo puede ser calculada como h × f(x), o si se conociera la función A(X), como A(x+h) − A(x). Estos valores son aproximadamente iguales para valores pequeños de h.
Supóngase ahora que se quiere calcular el área bajo la curva entre x y x+h. Se podría hacer hallando el área entre 0 y x+h y luego restando el área entre 0 y x. En resumen, el área de esta especie de "loncha" sería A(x+h) − A(x).
Otra manera de estimar esta misma área es multiplicar h por f(x) para hallar el área de un rectángulo que coincide aproximadamente con la "loncha". Nótese que la aproximación al área buscada es más precisa cuanto más pequeño sea el valor de h.
Por lo tanto, se puede decir que A(x+h) − A(x) es aproximadamente igual a f(x) · h, y que la precisión de esta aproximación mejora al disminuir el valor de h. En otras palabras, ƒ(x)·h ≈ A(x+h) − A(x), convirtiéndose esta aproximación en igualdad cuando h tiende a 0 como límite.
Dividiendo los dos lados de la ecuación por h se obtiene
Se muestra entonces de manera informal que ƒ(x) = A’(x), es decir, que la derivada de la función de área A(x) es en realidad la función ƒ(x). Dicho de otra forma, la función de área A(x) es la antiderivada de la función original.
Lo que se ha mostrado es que, intuitivamente, calcular la derivada de una función y "hallar el área" bajo su curva son operaciones "inversas", es decir el objetivo del teorema fundamental del cálculo integral.
Primer teorema fundamental del cálculo
Dada una función f integrable sobre el intervalo |
Demostración
Lema
Sea integrable sobre
integrable sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y
yDemostración del lema
Está claro que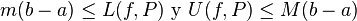 para toda partición
para toda partición  . Puesto que
. Puesto que  , la desigualdad se sigue inmediatamente.
, la desigualdad se sigue inmediatamente.Demostración
Por definición se tiene que .
.Sea h>0. Entonces
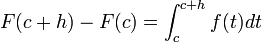 .
.Se define
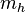 y
y 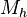 como:
como:-
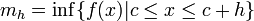 ,
,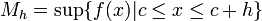
-
 .
.
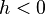 . Sean
. Sean-
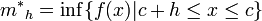 ,
,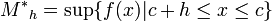 .
.
-
 .
.
-
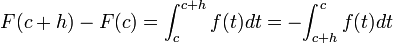 ,
,
-
 .
.
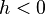 , se tiene que
, se tiene que-
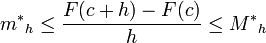 .
.
 es continua en c se tiene que
es continua en c se tiene que-
 ,
,
-
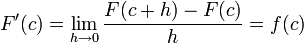 .
.
Ejemplos
Otra demostración
Cogiendo un intervalo cerrado![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) sobre
sobre ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , ya que
, ya que  es continua en
es continua en ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , también lo será en
, también lo será en ![[a,x]](https://upload.wikimedia.org/math/a/7/7/a7783208283b6aa11e1a07378a1ae7dc.png) .
.Según el teorema del valor medio para integrales se cumple que:
Haciendo el intervalo muy pequeño de tal manera que
 y debido a esa tendencia se tiene también que
y debido a esa tendencia se tiene también que 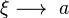
Por lo que en los límites se llega a:
Sabemos que :

Entonces la ecuación se la puede escribir como :
Dado que
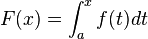 , entonces
, entonces 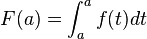
Y debido a que
 es continua en a, entonces
es continua en a, entonces 
Vista la ecuación de otra manera:
Por lo tanto
O también
Y en consecuencia
Con ello se demuestra el primer teorema fundamental del cálculo.
Segundo teorema fundamental del cálculo
El segundo teorema fundamental del cálculo integral (o regla de Newton-Leibniz, o también regla de Barrow, en honor al matemático inglés Isaac Barrow, profesor de Isaac Newton) es una propiedad de las funciones continuas que permite calcular fácilmente el valor de la integral definida a partir de cualquiera de las primitivas de la función.Enunciado
Dada una función f(x) continua en el intervalo [a,b] y sea F(x) cualquier función primitiva de f, es decir F '(x) = f(x). Entonces |
Demostración
Considere la siguiente primitiva de definida en el intervalo
definida en el intervalo ![[a,b]](https://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) .:
.:-
-
 .
.
-
-
-
![G'(x)=f(x) {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/c/1/c/c1c5b14eec3a07078372ecbb92a559e5.png) .
.
-
 y
y  son primitivas de
son primitivas de  , entonces
, entonces-
-
![\exists C \in \mathbb{R}: {\ }G(x)=F(x)+C, {\ } \forall x \in [a,b]](https://upload.wikimedia.org/math/b/7/7/b7724a98dad3e4e2b5116f519cf5708c.png) .
.
-
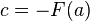 ; por lo tanto,
; por lo tanto,-
-
 .
.
-
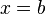 :
:Ejemplos
| (2015). Teorema Fundamental del cálculo. En: wikiped… Buscado elMartes, 10 de noviembre de 2015 Disponible en: https://es.wikipedia.org/wiki/Teorema_fundamental_del_c%C3%A1lculo |
| ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon. |

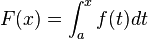 . Si f es
. Si f es  , entonces F es
, entonces F es  y F'(c) = f(c).
y F'(c) = f(c).
![m \leq f(x) \leq M \; \forall x \in [a,b]](https://upload.wikimedia.org/math/1/e/1/1e1b2ad811ce2c15f191c634ded2afd9.png)





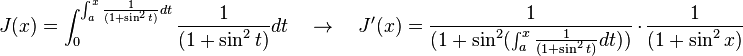
![\exists \xi\in[a,x]
: \quad
f(\xi)=
\frac{1}{x-a}\int_{a}^{x}f(t)dt](https://upload.wikimedia.org/math/f/c/c/fcc1b09852259ebc9a49ff937d0fe4ca.png)





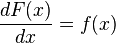


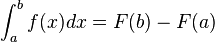
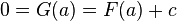

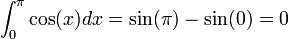
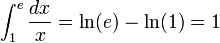
0 comentarios:
Publicar un comentario