2.2 Integral indefinida. |
Integración indefinida
El campo vectorial definido asignando a cada punto (x, y) un vector que tiene por pendiente ƒ(x) = (x3/3)-(x2/2)-x. Se muestran tres de las infinitas primitivas de ƒ(x) que se pueden obtener variando la constante de integración C.
Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.
Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F1 y F2 son dos primitivas de f, entonces existe un número real C, tal que F1 = F2 + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:
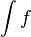 ó
ó 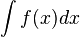
Índice
- 1 Ejemplo
- 2 Constante de integración
- 3 Otras propiedades
- 3.1 Linealidad de la integral indefinida
- 3.2 La primitiva de una función impar es siempre par
- 3.3 La primitiva F de una función f par es impar con tal de imponerse F(0) = 0
- 3.4 La primitiva de una función periódica es la suma de una función lineal y de una función periódica
- 3.5 Relación entre la integral de una función y la de su recíproca
- 3.6 Existencia de primitivas
- 4 Cálculo de primitivas
- 5 Véase también
- 6 Enlaces externos
Ejemplo
Una primitiva de la función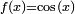 en
en 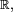 es la función
es la función  ya que:
ya que:Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales como sin(x), sin(x) + 5, sin(x) - 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma sin(x) + C donde C es una constante conocida como constante de integración.
Constante de integración
La derivada de cualquier función constante es cero. Una vez que se ha encontrado una primitiva F, si se le suma o resta una constante C, se obtiene otra primitiva. Esto ocurre porque (F + C) ' = F ' + C ' = F ' + 0 = F '. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.Para interpretar el significado de la constante de integración se puede observar el hecho de que la función f (x) es la derivada de otra función F (x), es decir, que para cada valor de x, f (x) le asigna la pendiente de F (x). Si se dibuja en cada punto (x, y) del plano cartesiano un pequeño segmento con pendiente f (x), se obtiene un campo vectorial como el que se representa en la figura de la derecha. Entonces el problema de encontrar una función F (x) tal que su derivada sea la función f (x) se convierte en el problema de encontrar una función de la gráfica de la cual, en todos los puntos sea tangente a los vectores del campo. En la figura de la derecha se observa como al variar la constante de integración se obtienen diversas funciones que cumplen esta condición y son traslaciones verticales unas de otras.
Otras propiedades
Linealidad de la integral indefinida
La primitiva es lineal, es decir:- Si f es una función que admite una primitiva F sobre un intervalo I, entonces para todo real k, una primitiva de kf sobre el intervalo I es kF.
- Si F y G son primitivas respectivas de dos funciones f y g, entonces una primitiva de f + g es F + G.
La primitiva de una función impar es siempre par
En efecto, como se ve en la figura siguiente, las áreas antes y después de cero son opuestas, lo que implica que la integral entre -a y a es nula, lo que se escribe así: F(a) - F(-a) = 0, F siendo una primitiva de f, impar. Por lo tanto siempre tenemos F(-a) = F(a): F es par.La primitiva F de una función f par es impar con tal de imponerse F(0) = 0
En efecto, según la figura, las áreas antes y después de cero son iguales, lo que se escribe con la siguiente igualdad de integrales:Es decir F(0) - F(-a) = F(a) - F(0). Si F(0) = 0, F(-a) = - F(a): F es impar.
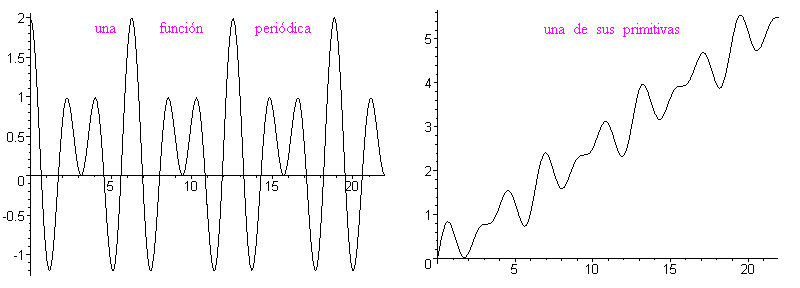
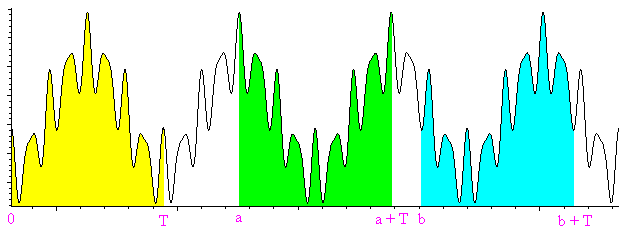
La primitiva de una función periódica es la suma de una función lineal y de una función periódica
Para probarlo, hay que constatar que el área bajo una curva de una función periódica, entre las abcisas x y x + T (T es el período) es constante es decir no depende de x. La figura siguiente muestra tres áreas iguales. Se puede mostrar utilizando la periodicidad y la relación de Chasles, o sencillamente ¡con unas tijeras! (cortando y superponiendo las áreas de color).En término de primitiva, significa que F(x + T) - F(x) es una constante, que se puede llamar A. Entonces la función G(x) = F(x) - Ax/T es periódica de período T. En efecto G(x + T) = F(x + T) - A(x + T)/T = F(x) + A - Ax/T - AT/T = F(x) - Ax/T = G(x). Por consiguiente F(x) = G(x) + Ax/T es la suma de G, periódica, y de Ax/T, lineal.
Relación entre la integral de una función y la de su recíproca
Para simplificar, se impone f(0) = 0; a es un número cualquiera del dominio de f. Entonces tenemos la relación:El área morada es la integral de f, el área amarilla es la de f -1, y la suma es el rectángulo cuyos costados miden a y f(a) (valores algebraicos). Se pasa de la primera curva, la de f, a la segunda, la de f -1 aplicando la simetría axial alrededor de la diagonal y = x.
El interés de esta fórmula es permitir el cálculo de la integral de f -1 sin conocer una primitiva; de hecho, ni hace falta conocer la expresión de la recíproca.
Existencia de primitivas
Cualquier función continua sobre admite localmente una antiderivada o primitiva. Sin embargo en espacios
de dimensión finita la continuidad no garantiza la existencia de
antiderivadas. Una condición suficiente de existencia de antiderivadas
es que la imagen pertenezca a un espacio vectorial conveniente, también llamado
admite localmente una antiderivada o primitiva. Sin embargo en espacios
de dimensión finita la continuidad no garantiza la existencia de
antiderivadas. Una condición suficiente de existencia de antiderivadas
es que la imagen pertenezca a un espacio vectorial conveniente, también llamado  -completo. La propiedad definitoria de dichos espacios es que toda función
-completo. La propiedad definitoria de dichos espacios es que toda función 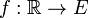 con
con 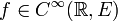 admite una función primitiva. Si el espacio no es
admite una función primitiva. Si el espacio no es  -completo la continuidad o incluso la suavidad de una función no garantiza la existencia de antiderivadas.
-completo la continuidad o incluso la suavidad de una función no garantiza la existencia de antiderivadas.Cálculo de primitivas
Integrales inmediatas
Para encontrar una primitiva de una función dada, basta con descomponerla (escribirla bajo forma de una combinación lineal) en funciones elementales cuyas primitivas son conocidas o se pueden obtener leyendo al revés una tabla de derivadas, y luego aplicar la linealidad de la integral:Función  : primitiva de : primitiva de 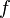 |
función 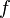 : derivada de : derivada de  |
|---|---|
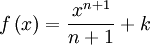 |
 |
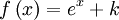 |
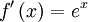 |
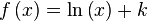 |
 |
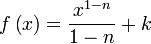 |
 |
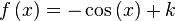 |
 |
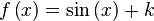 |
 |
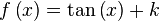 |
 |
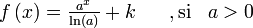 |
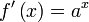 |
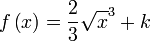 |
 |
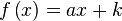 |
 |
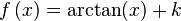 |
 |
Métodos de integración
Tenemos varios métodos a nuestra disposición:- La linealidad de la integración nos permite descomponer integrales complicadas en otras más sencillas.
- Integración por sustitución, a menudo combinada con identidades trigonométricas o el logaritmo neperiano.
- Integración por partes para integrar productos de funciones.
- El método de la regla de la cadena inversa, un caso especial de la integración por sustitución.
- El método de fracciones parciales nos permite integrar todas las funciones racionales (fracciones de dos polinomios).
- El algoritmo de Risch.
- Integrales también pueden calcularse utilizando tablas de integrales.
| (2015). Integral indefinida.En: wikiped… Buscado elMartes, 10 de noviembre de 2015 Disponible en: https://es.wikipedia.org/wiki/Integraci%C3%B3n_indefinida |
| ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon. |

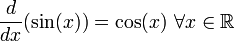




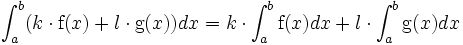
0 comentarios:
Publicar un comentario