4.1.5 Eliminación de Gauss y Gauss-Jordan. |
| El objetivo general de esta materia Matemáticas II es brindarnos nuevos conocimientos de nuevos temas aplicados en ella, como: Eliminación de Gauss y Gauss-Jordan. |
En matemáticas, la eliminación de Gauss-Jordan, llamada así debido a Carl Friedrich Gauss y Wilhelm Jordan, es un algoritmo del álgebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.
Índice
Antecedentes
El método de eliminación de Gauss aparece en el capítulo ocho del importante texto matemático chino Jiuzhang suanshu o Los nueve capítulos sobre el arte matemático. Su uso se ilustra en dieciocho problemas, con de dos a cinco ecuaciones. La primera referencia al libro por este título data del 179 DC, pero algunas de sus partes fueron escritas tan pronto como alrededor del 150 a. C.1 2 Fue comentado por Liu Hui en el siglo tercero.Análisis de su complejidad
La complejidad computacional de la eliminación gaussiana es de aproximadamente n3. Esto es, el número de operaciones requeridas es del orden de n3 si el tamaño de la matriz es n × n.Algoritmo de eliminación de Gauss-Jordan
- Ir a la columna no cero extrema izquierda
- Si el primer renglón tiene un cero en esta columna, intercambiarlo con otro que no lo tenga.
- Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados del renglón superior a los renglones debajo de él.
- Cubrir el renglón superior y repetir el proceso anterior con la submatriz restante. Repetir con el resto de los renglones (en este punto la matriz se encuentra en forma escalonada).
- Comenzando con el último renglón no cero, avanzar hacia arriba: para cada renglón obtener un 1 delantero e introducir ceros arriba de éste sumando múltiplos correspondientes a los renglones correspondientes.
Ejemplo
Supongamos que es necesario encontrar los números "x", "y", "z", que satisfacen simultáneamente estas ecuaciones:- Multiplicar una ecuación por un escalar no nulo.
- Intercambiar de posición dos ecuaciones
- Sumar a una ecuación un múltiplo de otra.
En nuestro ejemplo, eliminamos x de la segunda ecuación sumando 3/2 veces la primera ecuación a la segunda y después sumamos la primera ecuación a la tercera. El resultado es:
Primero:
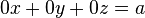 , donde a ≠ 0. Es decir,
, donde a ≠ 0. Es decir, 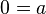 , lo que supone una contradicción y, por tanto, no tiene solución.
, lo que supone una contradicción y, por tanto, no tiene solución.Forma escalonada y escalonada reducida
Dos formas especiales de matrices son la escalonada y la escalonada reducida. Una matriz puede tener las siguientes propiedades:- Todas las filas 1 están en la parte inferior de la matriz.
- El elemento delantero de cada fila diferente de cero, éste es llamado "pivote"; éstos están a la derecha del elemento delantero de la fila anterior (esto supone que todos los elementos debajo de un pivote son cero).
- Todos los elementos delanteros ("pivotes") son iguales a 1
- Todos los elementos por encima de los pivotes son nulos.
Una vez que la matriz del sistema se ha transformado hasta obtener una matriz escalonada reducida es muy fácil discutirlo (es decir, determinar cuántas soluciones tiene):
- Cuando aparece un pivote en la columna de los términos independientes el sistema es incompatible (no tiene ninguna solución).
- En otro caso el sistema es compatible. Si además el número de pivotes coincide con el número de incógnitas el sistema es compatible determinado (tiene una única solución). Cuando el número de pivotes es menor que el número de incógnitas el sistema es indeterminado (tiene infinitas soluciones que dependen de tantos parámetros como indique la diferencia entre el número de incógnitas y el número de pivotes).
Otras aplicaciones
Encontrar la inversa de una matriz
Es posible usar la eliminación gaussiana para encontrar inversas de matrices n × n. Para ello se aumenta la matriz dada, digamos A con una matriz identidad, simplemente escribiendo las filas de la identidad a continuación de las de nuestra matriz A, por ejemplo dada:| (2015). Eliminación de Gauss y Gauss-Jordan.En: wikiped… Buscado elMartes, 10 de noviembre de 2015 Disponible en: https://es.wikipedia.org/wiki/Eliminaci%C3%B3n_de_Gauss-Jordan |
| ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon. |
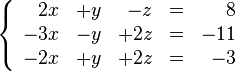


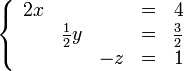

![\left [
\begin{array}{rrrr}
2 & 1 & -1 & 8 \\
-3 & -1 & 2 & -11 \\
-2 & 1 & 2 & -3
\end{array}
\right ]](https://upload.wikimedia.org/math/b/7/5/b75b0e02a527cf69e6f42dbd2fe2960f.png)
![\left [
\begin{array}{rrrr}
2 & 0 & 0 & 4 \\
0 & 1/2 & 0 & 3/2 \\
0 & 0 & -1 & 1
\end{array}
\right ]](https://upload.wikimedia.org/math/e/b/f/ebf74f6593b310153d2a6700d2f37b43.png)
![\left [
\begin{array}{rrrr}
1 & 0 & 0 & 2 \\
0 & 1 & 0 & 3 \\
0 & 0 & 1 & -1
\end{array}
\right ]](https://upload.wikimedia.org/math/d/4/0/d40cfce339ef9bb6dde8739c55d238d3.png)
![\left [ \begin{array}{cccc}
0 & 0 & 0 & a \\
\end{array} \right ]](https://upload.wikimedia.org/math/4/e/a/4ea82b742b346fc121881fd94c0d3d0c.png)
![\left [ \begin{array}{ccccc}
0 & 1 & 4 & 0 & 0 \\*
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1 \\
1 & 1 & 2 & 2& 2 \\
\end{array} \right ]](https://upload.wikimedia.org/math/c/b/0/cb0b990dc1dfc1136084b1cad16bec9b.png)
![A= \left [ \begin{array}{rrr}
2 & 1 & -1 \\
-3 & -1 & 2 \\
-2 & 1 & 2
\end{array} \right ]](https://upload.wikimedia.org/math/a/a/0/aa052c3d448ab767e4804a08e1093c27.png)
![\left [ \begin{array}{rrr|rrr}
2 & 1 & -1 & 1 & 0 & 0 \\
-3 & -1 & 2 & 0 & 1 & 0 \\
-2 & 1 & 2 & 0 & 0 & 1
\end{array} \right ]](https://upload.wikimedia.org/math/9/e/a/9eacbd40cfec5f75f6738cab4ab63fdb.png)
![\left [ \begin{array}{ccc|ccc}
\,\,\,\, 2 & 1 & -1 & 1 & 0 & 0 \\
-1 & 0 & \,\,\,\, 1 & 1 & 1 & 0 \\
\,\,\,\, 0 & 2 & \,\,\,\, 1 & 1 & 0 & 1
\end{array} \right ]](https://upload.wikimedia.org/math/a/8/7/a8745bf66474415b1e30ac2cf008ef0b.png)
![\left [ \begin{array}{ccc|ccc}
1 & 0 & -1 & -1 & -1 & 0 \\
2 & 1 & -1 & \,\,\,\,1 & \,\,\,\, 0 & 0 \\
0 & 2 & \,\,\,\, 1 & \,\,\,\,1 & \,\,\,\, 0 & 1
\end{array} \right ]](https://upload.wikimedia.org/math/2/c/d/2cd44bd6fb5234a54ca159fb5b4d2c99.png)
![\left [ \begin{array}{ccc|ccc}
1 & 0 & -1 & -1 & -1 & 0 \\
0 & 1 & \,\,\,\,1 &\,\,\,\, 3 & \,\,\,\, 2 & 0 \\
0 & 2 & \,\,\,\, 1 & \,\,\,\, 1 & \,\,\,\, 0 & 1
\end{array} \right ]](https://upload.wikimedia.org/math/3/b/7/3b7068abe5bd12c3b4537ab4fdeacc95.png)
![\left [ \begin{array}{ccc|ccc}
1 & 0 & -1 & -1 & -1 & 0 \\
0 & 1 & \,\,\,\, 1 & \,\,\,\,3 & \,\,\,\, 2 & 0 \\
0 & 0 & -1 & -5 & -4 & 1
\end{array} \right ]](https://upload.wikimedia.org/math/1/a/0/1a03f0c046ae7ca419033fd7eb2cfcdc.png)
![\left [ \begin{array}{ccc|ccc}
1 & 0 & 0 &\,\,\,\, 4 & \,\,\,\, 3 & -1 \\
0 & 1 & 0 & -2 & -2 &\,\,\,\, 1 \\
0 & 0 & 1 & \,\,\,\, 5 & \,\,\,\, 4 & -1
\end{array} \right ]](https://upload.wikimedia.org/math/2/5/f/25fc3e620c741de3675609c779c1d3c8.png)
0 comentarios:
Publicar un comentario