2015 ~ Mate2

4.3.4 Regla de Cramer.

El objetivo general de esta materia Matemáticas II es brindarnos nuevos conocimientos de nuevos temas aplicados en ella, como: Regla de Cramer.

La regla de Cramer es un teorema del álgebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752), quien publicó la regla en su Introduction à l'analyse des lignes courbes algébriques de 1750, aunque Colin Maclaurin también publicó el método en su Treatise of Geometry de 1748 (y probablemente sabía del método desde 1729).¹
La regla de Cramer es de importancia teórica porque da una expresión explícita para la solución del sistema. Sin embargo, para sistemas de ecuaciones lineales de más de tres ecuaciones su aplicación para la resolución del mismo resulta excesivamente costosa: computacionalmente, es ineficiente para grandes matrices y por ello no es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para matrices pequeñas, particularmente cuando son usadas operaciones SIMD.
Si

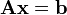\mathbf{Ax} = \mathbf{b}

es un sistema de ecuaciones.

\mathbf{A}

es la matriz de coeficientes del sistema,

\mathbf{x} = (x_1,\dots,x_n)

es el vector columna de las incógnitas y

\mathbf{b}

es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:

x_j = \cfrac { \det(\mathbf{A}_j) }{ \det(\mathbf{A}) }

donde

\mathbf{A}_j

es la matriz resultante de reemplazar la j-ésima columna de

\mathbf{A}

por el vector columna

\mathbf{b}

. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz

\mathbf{A}

ha de ser no nulo.

Índice

Sistema de 2x2

Para la resolución de un sistema de dos ecuaciones con dos incógnitas, de la forma. Dado el sistema de ecuaciones:

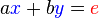
a{\color{blue}x}+b{\color{blue}y} = {\color{red}e}\,

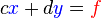
c{\color{blue}x}+d{\color{blue}y} = {\color{red}f}\,

Se representa matricialmente :

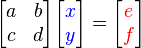
\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} {\color{blue}x} \\ {\color{blue}y} \end{bmatrix} = \begin{bmatrix} {\color{red}e} \\ {\color{red}f} \end{bmatrix}

Entonces,

x

y

pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:

x = \frac { \begin{vmatrix} \color{red}{e} & b \\ \color{red}{f} & d \end{vmatrix} }{ \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = \frac{ {\color{red} e } d - b {\color{red} f } }{ ad - bc }; \quad y = \frac { \begin{vmatrix} a & \color{red}{e} \\ c & \color{red}{f} \end{vmatrix} }{ \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = \frac{ a{\color{red} f } - {\color{red} e } c }{ ad - bc }

Ejemplo

Ejemplo de la resolución de un sistema e de 2x2:
Dado

3x+1y = 9\,

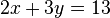
2x+3y = 13\,

que matricialmente es:

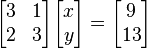
\begin{bmatrix} 3 & 1 \\ 2 & 3 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} 9 \\ 13 \end{bmatrix}

x e y pueden ser resueltos usando la regla de Cramer

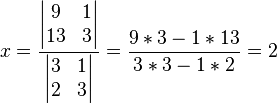
x = \frac { \begin{vmatrix} 9 & 1 \\ 13 & 3 \end{vmatrix} } { \begin{vmatrix} 3 & 1 \\ 2 & 3 \end{vmatrix} } = { 9*3 - 1*13 \over 3*3 - 1*2} = 2

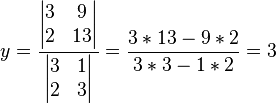
y = \frac { \begin{vmatrix} 3 & 9 \\ 2 & 13 \end{vmatrix} } { \begin{vmatrix} 3 & 1 \\ 2 & 3 \end{vmatrix} } = { 3*13 - 9*2 \over 3*3 - 1*2} = 3

Sistema de 3x3

La regla para un sistema de 3x3, con una división de determinantes:

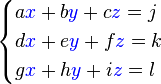
\begin{cases} a{\color{blue}x} + b{\color{blue}y} + c{\color{blue}z} = {\color{black}j}\\ d{\color{blue}x} + e{\color{blue}y} + f{\color{blue}z} = {\color{black}k}\\ g{\color{blue}x} + h{\color{blue}y} + i{\color{blue}z} = {\color{black}l} \end{cases}

Que representadas en forma de matriz es:

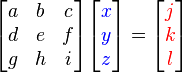
\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \begin{bmatrix} {\color{blue}x} \\ {\color{blue}y} \\ {\color{blue}z} \end{bmatrix} = \begin{bmatrix} {\color{red}j} \\ {\color{red}k} \\ {\color{red}l} \end{bmatrix}

x

y

z

pueden ser encontradas como sigue:

x = \frac { \begin{vmatrix} {\color{red}j} & b & c \\ {\color{red}k} & e & f \\ {\color{red}l} & h & i \end{vmatrix} }{ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} }; \quad y = \frac { \begin{vmatrix} a & {\color{red}j} & c \\ d & {\color{red}k} & f \\ g & {\color{red}l} & i \end{vmatrix} }{ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} } , \quad z = \frac { \begin{vmatrix} a & b & {\color{red}j} \\ d & e & {\color{red}k} \\ g & h & {\color{red}l} \end{vmatrix} }{ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} }

Ejemplo

Dado el sistema de ecuaciones lineales:

3x+2y+1z = 1\,

2x+0y+1z = 2\,

-1x+1y+2z = 4\,

expresado en forma matricial:

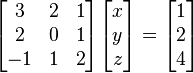
\begin{bmatrix} 3 & 2 & 1 \\ 2 & 0 & 1 \\ -1 & 1 & 2 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix}= \begin{bmatrix} 1\\ 2\\ 4 \end{bmatrix}

Los valores de

x, y \text{ y } z

serían:

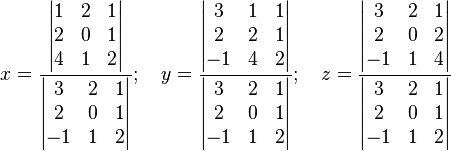
x= \frac { \begin{vmatrix} 1 & 2 & 1\\ 2 & 0 & 1\\ 4 & 1 & 2 \end{vmatrix} }{ \begin{vmatrix} 3 & 2 & 1\\ 2 & 0 & 1\\ -1 & 1 & 2 \end{vmatrix} } ; \quad y= \frac { \begin{vmatrix} 3 & 1 & 1\\ 2 & 2 & 1\\ -1 & 4 & 2 \end{vmatrix} }{ \begin{vmatrix} 3 & 2 & 1\\ 2 & 0 & 1\\ -1 & 1 & 2 \end{vmatrix} } ; \quad z= \frac { \begin{vmatrix} 3 & 2 & 1\\ 2 & 0 & 2\\ -1 & 1 & 4 \end{vmatrix} }{ \begin{vmatrix} 3 & 2 & 1\\ 2 & 0 & 1\\ -1 & 1 & 2 \end{vmatrix} }

Demostración

Sean:

\boldsymbol x = \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix} \quad \boldsymbol b = \begin{pmatrix} b_1 \\ \vdots \\ b_n \end{pmatrix}

\boldsymbol A_j = \left [ \begin{array}{llllllll} a_{1,1} & \cdots & a_{1,j-1} & b_1 & a_{1,j+1} & \cdots & a_{1,n} \\ a_{2,1} & \cdots & a_{2,j-1} & b_2 & a_{2,j+1} & \cdots & a_{2,n} \\ \\ \vdots & & & \ddots & & & \vdots \\ \\ a_{n-1,1} & \cdots & a_{n-1,j-1}& b_{n-1} & a_{n-1,j+1} & \cdots & a_{n-1,n} \\ a_{n,1} & \cdots & a_{n,j-1} & b_n & a_{n,j+1} & \cdots & a_{n,n} \end{array} \right ]

Usando las propiedades de la multiplicación de matrices:

\boldsymbol A \boldsymbol x = \boldsymbol b \Leftrightarrow \boldsymbol A^{-1} \boldsymbol A \boldsymbol x = \boldsymbol A^{-1} \boldsymbol b \Leftrightarrow \boldsymbol {Ix} = \boldsymbol A^{-1} \boldsymbol b \Leftrightarrow \boldsymbol x = \boldsymbol A^{-1} \boldsymbol b

entonces:

\boldsymbol x = \boldsymbol A^{-1} \boldsymbol b = \frac{ (\operatorname{Adj} \boldsymbol A)^t }{ \left| \boldsymbol A \right| } \; \boldsymbol b

(\operatorname{Adj}\boldsymbol A)^t = \frac{\boldsymbol A^\prime_{pl}}{\boldsymbol A^\prime_{pl}} = \boldsymbol A_{lp}

Por lo tanto:

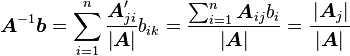
\boldsymbol A^{-1} \boldsymbol b = \sum_{i=1}^n \frac{ \boldsymbol A^\prime_{ji} }{ \left | \boldsymbol A \right | } b_{ik} = \frac{ \sum_{i=1}^n \boldsymbol A_{ij} b_i }{ \left | \boldsymbol A \right | } = \cfrac { \left | \boldsymbol A_j \right | }{ \left | \boldsymbol A \right | }

Aparte, recordando la definición de determinante, la suma definida acumula la multiplicación del elemento adjunto o cofactor de la posición

ij

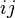, con el elemento i-ésimo del vector

\boldsymbol B

(que es precisamente el elemento i-èsimo de la columna

j

, en la matriz

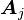\boldsymbol {A}_j

(2015). Regla de Cramer.En: wikiped… Buscado elMartes, 10 de noviembre de 2015 Disponible en: https://es.wikipedia.org/wiki/Regla_de_Cramer

ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon.

4.3.3 Propiedades de los determinantes.

El objetivo general de esta materia Matemáticas II es brindarnos nuevos conocimientos de nuevos temas aplicados en ella, como: Propiedades de los determinantes.

|A^t|= |A|

El determinante de una matriz A y el de su traspuesta A^t son iguales.

2 |A| = 0 Si:

Posee dos filas (o columnas) iguales.

Todos los elementos de una fila (o una columna) son nulos.

Los elementos de una fila (o una columna) son combinación lineal de las otras.

F₃ = F₁ + F₂

3 Un determinante triangular es igual al producto de los elementos de la diagonal principal.

4 Si en un determinante se cambian entre sí dos filas (o dos columnas), su valor sólo cambia de signo.

5 Si a los elementos de una fila (o una columna) se le suman los elementos de otra multiplicados previamente por un número real, el valor del determinante no varía.

Es decir, si una fila (o una columna) la transformamos en una combinación lineal de las demás, el valor del determinante no varía.

6 Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier fila (o cualquier columna), pero sólo una.

7 Si todos los elementos de una fila (o columna) están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes en los que las demás filas (o columnas) permanecen invariantes.

8 |A · B| =|A| · |B|

El determinante de un producto es igual al producto de los determinantes.

(2015). Propiedades de los determinantes.En: vitutor… Buscado elMartes, 10 de noviembre de 2015 Disponible en: http://www.vitutor.com/algebra/determinantes/propiedades.html

ARYA, J. C. (2009). Matemáticas aplicadas a la administración. México: Pearson Educacíon.

Mate2

martes, 1 de diciembre de 2015

¿Para que podemos usar lo aprendido en el periodo?

Objetivo

sábado, 28 de noviembre de 2015

4.3.4 Regla de Cramer.

4.3.4 Regla de Cramer.

Índice

Sistema de 2x2

Ejemplo

Sistema de 3x3

Ejemplo

Demostración

4.3.3 Propiedades de los determinantes.

4.3.3 Propiedades de los determinantes.

Páginas

Popular Posts

Recent Posts

Unordered List

Pages

Text Widget

Blog Archive

About

Blogger templates

Sample Text